On what basis I don’t recall, I was led into the contemplation of the generalized process of “cuboctization” which produces the cuboctahedron from the octahedron. This process is namely the connection of the midpoints of “neighboring” edges, to produce a new figure with vertices at these midpoints, and with the constructed edges.

It’s important to note that this figure, being composed of vertices and edges, is not necessarily a geometric solid, since the new vertices may not lie in a plane, to form a face. Nevertheless, we may proceed.

Of course the founding idea is the production from the octahedron

of the cuboctahedron, which may be regarded as a truncation of the octahedron, but in this case can be regarded as being produced in the manner described.

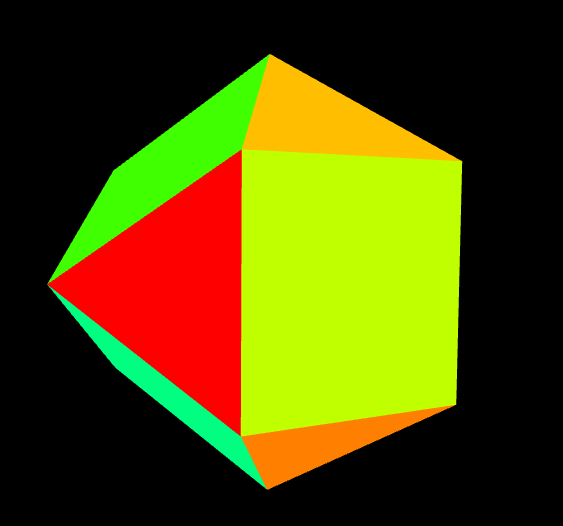
So we may proceed in this manner, and to arrive at the nub of the discussion in short order, we may present “cubocta5”, the result of applying the algorithm of edge midpoint connection four more times.

But here we have run aground. You can see that the four expected quadrilateral faces next to the green quadrilateral face in the center have been “bent”. Their defining vertices did not lie in a plane. We may remind ourselves that our procedure did not have any reference to faces at all, but only vertices and edges, so that we were only lucky up to this point to produce flat, or planar, four sided faces.

… but it’s close! So, what to do? Can we “flatten” these faces somehow, and produce a true cubocta5 polyhedron?

Never fear! A way was found. By retreating to the cubocta2, and adjusting the position of the vertices, we produced this version

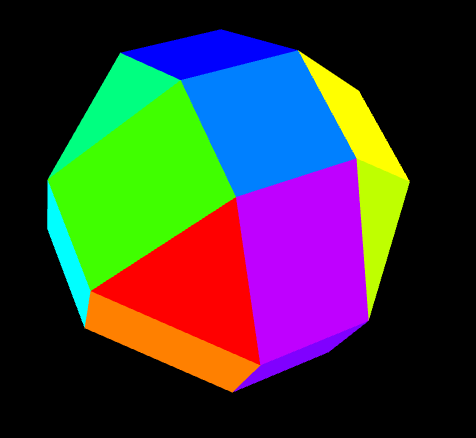
All on a hunch, if you will. But that’s not half the story! At any rate, three iterations of our edge production algorithm produce the desired result. A truly remarkable figure with 192 vertices, 384 edges, and 194 faces. 8 of these faces are small triangles at the corners of a cube, and the remainder are quadrilaterals of varying proportions, but all perfectly flat.

If this figure “exists in the literature”, we would like to know, but at any rate, this version of it is original with us.

Some Numerology

It’s additionally remarkable that the entire figure can be specified in terms of small integers for the coordinates of the vertices, and there are only six distinct vertices required to produce the entire figure under octahedral symmetry. Here they are with the number of replications:

(24) 10 6 0
(24) 12 2 0
(48) 11 4 2
(24) 8 8 2
(48) 9 6 4
(24) 7 7 6

The 48 replications are the 6 permutations of the values times the 8 versions of each obtained by taking +/- each value, in combination.

since +/- 0 = 0, there are only 4 sign combinations for 10 6 0 and 12 2 0, and in the case of 8 8 2 and 7 7 6 there are only 3 distinct permutations, times the 8 sign combinations. Of course these add to 192.