The passage of 2014 DX110 is just the latest in a series of near earth encounters that have been observed, and it raises the question, what is the likelihood of one of these actually hitting the earth, supposing a continuing sequence of them? Of course this has been going on for a long time, and they DO occasionally hit the earth, but how might we model these encounters statistically?
Let’s take the lunar orbit standard and suppose that a medium sized asteroid passes within “the lunar hoop” perpendicular to its relative direction of motion, say once a year. Then if each of these objects has a constant probability per unit area of passing through a particular point in the hoop, we need only compare the cross section of the earth to the size of the hoop to estimate the fraction of these encounters that result in a collison with the earth, and this fraction is just the square ratio of the earth’s radius to the moon’s orbit, or about 1/602 = 1/3600 .
Gravitational Focusing
But then we might ask, what about the gravitational attraction of the earth? Wouldn’t it tend to “focus” objects passing nearby and increase the effective collision radius?
I think the answer is “somewhat”, but there is a simple treatment of the problem that is interesting more for the understanding it affords than any modification of such an estimate.
Let’s directly apply conservation of energy and angular momentum to get a simple and exact answer to the idealized “two body problem” of a small object passing by the earth in an inertial frame of reference. This is actually a reasonable approximation, I think.
Conservation of energy is expressed by
1/2 v2 – MG/r = constant
and conservation of momentum is expressed by
v rperp = constant
In particular, if an object approaches the earth from a great distance with speed v1 and s is its projected straight line distance of closest approach ( measured to the center of the earth, ) then its angular momentum wrt the center of the earth is v1 s , and if r0 is the actual hyperbolic distance of closest approach, where it has velocity v0, we must have
v1 s = v0 r0
A hyperbolic Interlude
The situation is illustrated in the following diagram, which shows the hyperbolic path of an object passing the earth ( in blue ) and the asymptotes of the hyperbola in gray:
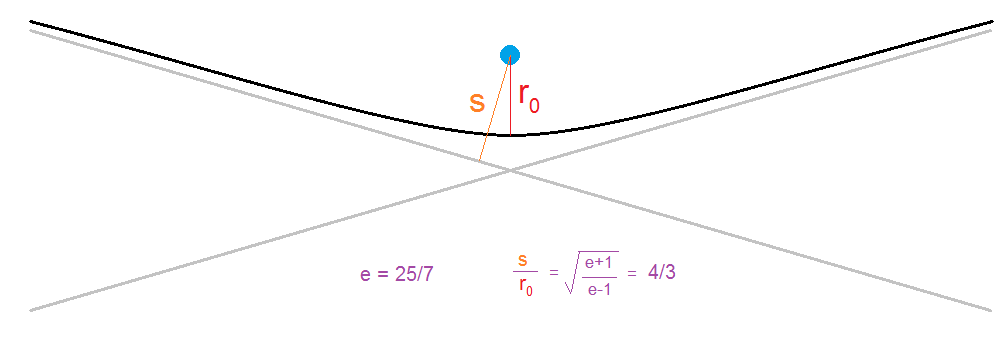
The diagram has been drawn to scale for a hyperbola with parameters a=7, b=24, which gives the focal distance of sqrt( 72+242 ) = 25, and hence the rational eccentricity of 25/7 . It’s part of a sequence of pythagorean triples with the lowest element being the sequence of odd integers beginning with three, and the two larger elements differing by 1 ..
3 4 5
5 12 13
7 24 25
9 40 41
…
This is of purely heuristic interest, but it gives us a sequence of “rationalized” hyperbolas with linearly increasing eccentricity.
Note that our ratio of interest, s/r0 , is also rational. 7 24 25 is the 3rd entry in the list, and the generalization holds that this ratio is (n+1)/n for the nth entry. We’ll come back to this …
Dynamics continued
We can simplify our notation by an appropriate choice of units. We note that the formula for conservation of energy, with constant set to zero :
1/2 ve2 – MG/re = 0
or
1/2 ve2 = MG/re
… is the defining equation for the escape velocity from the surface of the earth, and we can express the potential energy in terms of the escape velocity:
MG/r0 = 1/2 ( re / r0 ) ve2
Then if we measure r in units of re, and v in units of ve, Conservation of energy between the far motion at velocity v1 and zero potential energy, and the close approach v0 can be simply expressed as:
v12 = v02 – 1/r0
Note we have “multiplied through by 2” to get rid of the factor of 1/2 in each term.
Now we can use the equation for conservation of angular momentum to express v0 in terms of v1, or vice versa, and with some elementary rearrangement of terms we get these two equations for s in terms of r0 and v1, or r0 and v0 :
s2 = r02 ( 1 + 1/ ( r0 v12 ) ) = r02 / ( 1 – 1/ ( r0 v02 ) )
Notice that for large v1, i.e. much greater than earth escape velocity ( implying large v0 as well,) we have r0 = s, so the object just zooms right by. Otherwise, we have an easy formula for determining s in terms of r0 and v1 or v0 .
Impact criterion
If we set r0 = 1, i.e. the radius of the earth, we have a very simple formula for the apparent or effective size of the earth in terms of v1, expressed in units of earth escape velocity.
s = sqrt( 1 + v1-2 )
For example, for the earth to “appear” twice its diameter, the incoming speed would have to be 1/sqrt(3) = .58 , or 58% of earth escape velocity.
The case of 2014 DX110
Well what about 2014 DX110 ? It’s stated that its flyby speed was 33000 mph or 14.7 km/sec, compared to 11.2 km/sec, so v0 = 1.3125
It came within 54 earth radii at close approach meaning r0 = 54, and we can use the v0 version of our formula to get
s = 54 / sqrt( 1 – 1/ ( 54 x 1.31252 ) ) = 54 x 1.0054
s/r0 = 1.0054
… and finally
To find a rationalized hyperbola which “approaches” this case, we note ( as per above ) that (n+1)/n = 1 + 1/n, so we want n = 1/0.0054 ~= 185, so we take the 185th in the sequence of Pythagorean triples:
371 68820 68821
and eccentricty e = 68821/371 ~= 185.5
