Because … just look at the guy!

Looks like a regular barrel of monkeys!
He is the namesake of Faulhaber’s Formula, although he did not formulate it, as Wikipedia points out, but he more than laid the groundwork, I think anyone would agree.
Unbeknowst to myself, I had been following in his footsteps ( a very short way, of course ) in my pursuit of mathematical diversions. His namesake formula is a generalization of the idea of finding a formula for the sum of integers, from 1 to N, each taken to a given power. Familar to many is the formula for the sum of integers, i, from 1 to N, which is remembered as “first plus last times n over 2” or with these fixed limits, N(N+1)/2 .
I had presented this rule in graphical form as :
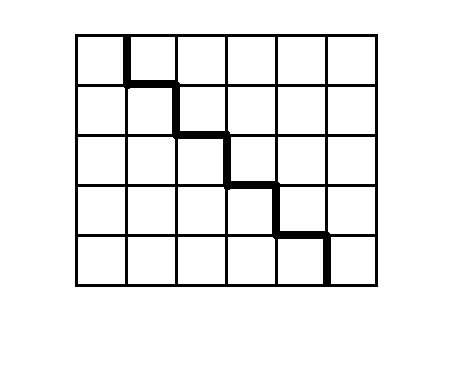
Showing an N by N+1 rectangle divided into 2 pieces, each representing
the sum of 1 thru 5.
So, I had the thought of representing the sum of the squares of integers in like manner, and made these model pieces.

I originally made 3 pieces, and noticed that these fitted readily into the following form, noting that there is a left handed and a right handed version, even though each piece is mirror-symmetric:
So then with due attention to “handedness”, ( do we need same, or opposite ? … ) we get this result:
Noting that the bottom square of each piece is N x N, with N=7 in this case, you can see from the picture that the block thus formed is N x ( N + 1 ) x (2 N + 1 ), so 1/6 th of this value gives the sum of integers from 1 thru N, each squared.
Moving right along
All this transpired some time ago, and I don’t believe that I got as far as the name of “Faulhaber” at that time, being content with my “physical derivation”. Just lately I pursued the issue a little further, going as far as N=3 and N=4, using simple algebra, much as Faulhaber must have done in some form or another, although he went all the way to N=17.
My method was to assume a formula, e.g. for N=2, of the form sum_1_to_N(i^2) =
a N^3 + b N^2 + c N + d , and then require that, sum( (i+1)^2 ) – sum( i^2 ) = (i+1)^2. It’s all just bookkeeping and I got the required answer, then I went to N=3 and did the same thing, and “discovered” ( for myself ) the “well known” result that the answer is simply ( N(N+1)/2 ) ^2 … amazing! I never knew!
Flushed with excitement, I realized that this lent itself to a simple 2-d graphical representation, which I worked out easily, and here it is:

Looking at the left and bottom edges, you can see the sequence of 1 2 3 4 5 6 7, in alternating colors, which immediately gives the “squared” result for the sum just cited.
Then looking at the red bands, you’ll see that these contain, in sequence, 1 1×1 square, 3 3×3 squares, 5 5×5 squares, and 7 7×7 squares, representing the cubes of the odd numbers. The blue bands represent the cubes of the even numbers in the same way, except that one square is split into two identical rectangles at each edge, a necessity required for an even number of squares.
So there it is! I don’t know where else you might find this kind of diagram, but this one is my own production, at least.


