… of course I allude to the punchline, “Consider a spherical horse”, although there is such a thing as a spherical square. Namely a quadrilateral drawn on the surface of a sphere with equal sides and equal angles. Many years ago I was drawn into contemplation of this by a statement in Peterson’s Field Guide to the Stars and Planets, by Donald Menzel, that “The sky contains approximately 40,000 square degrees …” as excerpted here:
A more accurate value is given by 4Pi/(Pi/180)2 = 41252.96125, but this is still approximate, as it does not allow for the curvature of the “square degree” itself. So I endeavored to derive an exact value for the area of a spherical square degree, and did so, as recorded in this note:
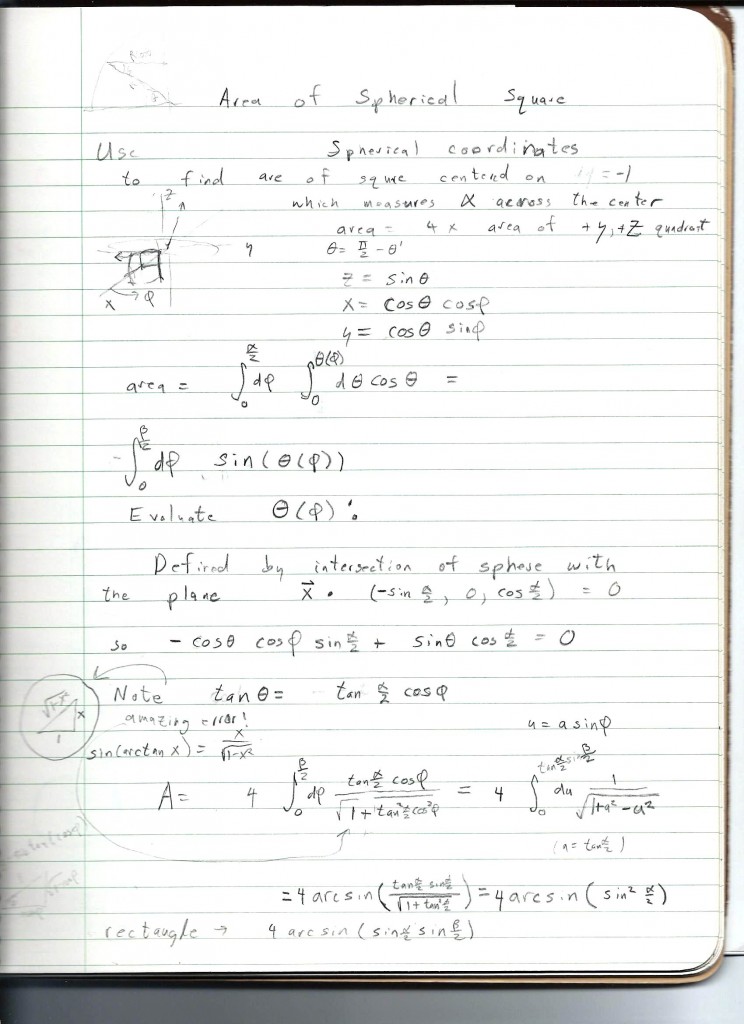
I was quite pleased with this result at the time, as it was simple and even had a certain elegance, and in fact I had difficulty reproducing the calculation before I rediscovered my note. I did remember the result verbally: “four arcsine of sine squared alpha over two”, where alpha is the measure of the square across the center.
Applying this formula gives the value of 41254.00842 for “square degrees in the sky”, differing by about 1 in the units place from the linear approximation.
I recall that I knew at the time that the formula was “four arcsine of tan squared beta over two”, where beta is a side of the square. This gives 41250.86683, undershooting the linear approx. by about twice the amount that the alpha formula overshoots. I’m sure there’s a story there, but let’s move on.
I was recently drawn into contemplation of the spherical square by a NYT Quote-acrostic based on a quote by Calvin Trillin, which alluded to the infamous Indiana Pi Bill ( misattributing it to Texas ). The cited Wiki article offered in explanation of the bill’s content, a crank mathematical screed, that “it is clear that the assertion is simply that the area of a circle is the same as that of a square with the same perimeter”
I started wondering if this might not be true for some spherical square and circle. I finally realized that it is true of the “degenerate” spherical square whose sides are quadrants of an equator, but too late! … I was back on the case.
In my calculation, I had retreated to the comfort zone of spherical coordinates, and resorted to integral techniques which, while well within the bounds of Introductory Calculus, were less than straightforward.
I knew that the problem could be solved by methods of Spherical Trigonometry, but I didn’t see that these were any simpler.
Well, this time around I came up with a simple construction that makes it a “one step problem” , applying the rule of “spherical excess” for the area of a spherical triangle:
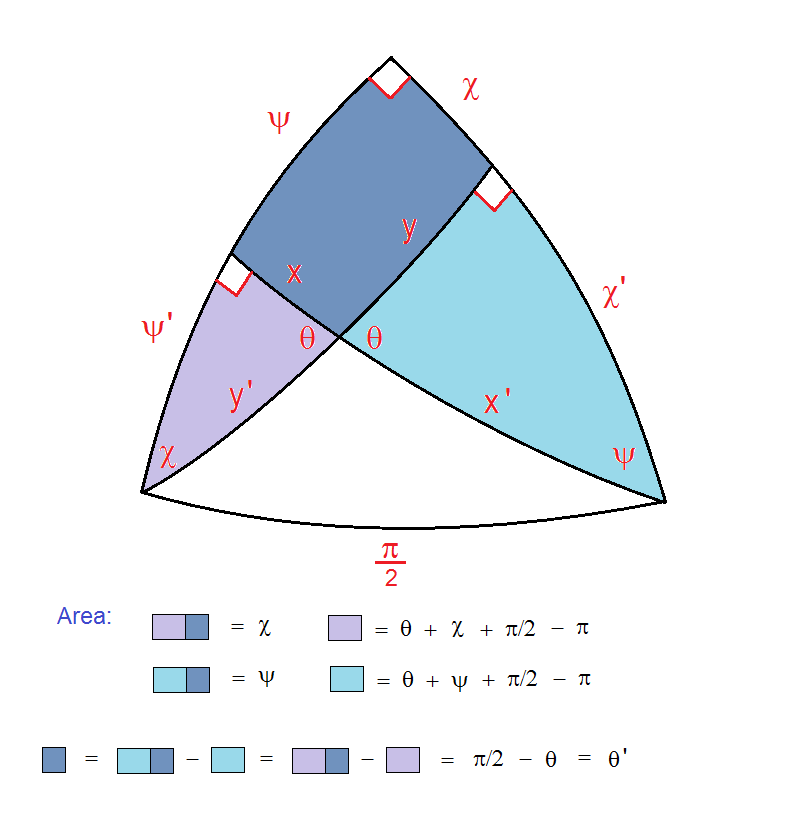
Well OK, a “two step problem”, we still have to solve for theta. This is an easy application of Napier’s rules for right spherical triangles applied to either the light blue or lavender auxillary diagram in the figure, and giving
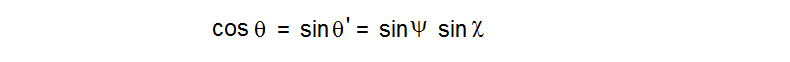
or …
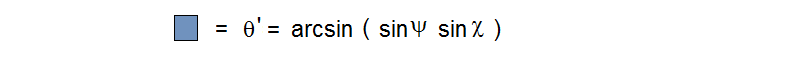
Additionally, we may solve for the distances x and y, which are the half-lengths of the sides of the spherical rectangle. Applying Napiers rules, as above, we get:
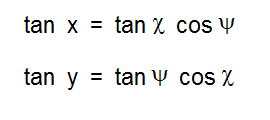
Note that when psi = chi and equivalently x = y, we have the identity
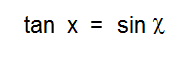
… as alluded to above.
