The relevance of Pascal’s Triangle to a “best of seven” tournament, such as the World Series, is obvious. But there is that wrinkle of not actually playing all seven games. In the past I had contented myself with various adjustments, but I never actually drew up “Pascal’s Diamond”, which is based very simply on the same generating rule as the Triangle, but terminated appropriately, as shown here:

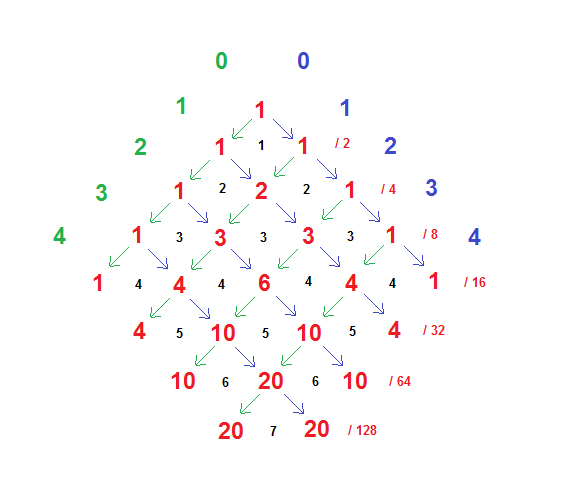
Note that it’s equivalent to Pascal’s Triangle up to game 4 ( as indicated by the black numbers ) but terminates along the diagonals indicating 4 wins by either team. We immediately see that the nominal probability ( assuming “chance” outcomes ) of a 4,5,6, or 7 game series is 1/8, 1/4, 5/16, or 5/16, respectively.

Note that the equal probability of a 6 or 7 game series is a reflection of the “chance” outcome of game 6, which terminates the series at 4-2, or forces a game 7 with equal probability.

I decided to compare these probabilities with the last 91 world series results, in terms of games played, or equivalently, “games won by the series loser”. I found these to be 18, 18, 20, and 35. This compares to a nominal expectation of 11.37, 22.74, 28.43, and 28.43, for 91 “chance” games. So, this looks a little out of whack! But is it really? …

Oh No! Not STATISTICS!

Well, we don’t have to do a canned analysis, even if we find ourselves being driven that way. We can make up any sort of test and apply it experimentally to sets of 91 “chance” series, and determine the “probability of rejecting the null hypothesis”, in this case the hypothesis that the real outcomes obey the same statistics as “chance” would have it.

Let’s just try looking at a generated sequence of 91 chance-ruled series. Here’s 10 of them, with the average over all 10 at the bottom. Each row represents the number of 4,5,6, and 7 game series in a trial of 91.

$ series 10
9 20 31 31
9 18 38 26
12 19 32 28
14 14 37 26
12 20 31 28
12 19 33 27
12 24 32 23
11 23 27 30
11 25 27 28
8 26 26 31

11.000 20.800 31.400 27.800

Well, notice the 14, 14, 37, 26 … qualitatively very similar to the actual historical “trial” of 91 world series, so impressionistically, we don’t have grounds to believe the games are ruled by anything but chance.

I’ll just add that I did go “back to the books”, or Wikipedia as we do these days, and tutored myself on some of the sigma-based statistical tests, and I’m ready to report that it’s all very interesting!