I mentioned the image gallery section of the Wiki Mandelbrot Set article as the starting point for my renewed interest in this topic. It is based on a zoom sequence terminating on a “Julia Island”, which is a component of the Mandelbrot set resembling a “Julia set”, which is based on the actual sequence of an iteration rather than the in/out criterion of the Mandelbrot set. So there’s a little math magic in this resemblance.

Here is my recreation of the zoom, based on the linked tool I mentioned, which by no means outstrips the images in the article ( which can be expanded, ) but it does go a little deeper, and it keeps the Julia Island location at center. This was easy to do by working backwards from the deepest image and keeping the same coordinates by simply changing the scale in the URL field.

Here’s a “hot link” of the lowest level of the Wiki zoom :( To see its full glory visit the site. ) It roughly corresponds to the antepenultimate frame of the animated gif. The commentary in the main article notes that there is a “satellite” ( i.e. “mini-Mandelbrot set” ) at the center of the island structure that is “too small to see at this magnification”. Just visible there is the large square structure in the center of the last frame of the gif, where you can almost see the satellite at the center of it, as a tiny dark speck.

This conclusion is supported, if not confirmed, by perusal of a nearby and entirely analogous structure, which is a little bit larger. Here’s a slower zoom, taking 1/2 per frame instead of 1/10, showing a descent through the analogous square structure to reveal the Mandelbrot satellite.

Note the emergence of a new “sea” of similar spirals and structures as part of the INFINITE descent. It’s fascinating and incredible and, like the song says, “a little bit frightening.”

I recently saw one of several “Deep Zoom” videos of the Mandelbrot set, which I’ll leave alone for now, but it got me interested in the subject, which I haven’t thought about since the 1980’s. Times change, and the facilities available for investigating the subject are now, of course, much more powerful. I looked at the Wikipedia article on the Mandelbrot set, which refreshed and greatly expanded my casual knowledge of the subject. The exciting thing though is the link under the section headed “Image gallery of a zoom sequence” to an “interactive viewer” ( go to Wikipedia to get the link. ) It indicates it will open for “this location” ( i.e. the one illustrated ) but I found it goes to the initial full view of the set.

Anyway, it’s a fabulous tool. You can click on a spot to zoom by a factor of two, and although it does take time to calculate the image, you can click again for repeated zooms without waiting for the full resolution. I found it very handy to use. It goes down to 10^-14 in scale, which is well short of the claims made by these deep zoom videos, but it provides ample scope for casual exploration.

Note the parameters are passed in the URL address field, and these can be edited and entered with the naturally hoped for result. Of course you can save them and reenter them to bring back the image, so as I say, very handy.

I also used the extended precision calculator, bc, on Cygwin to explore some of the mathematical aspects, which I’ll get to. First, here’s an animated gif of a short zoom on a large portion of the Mandelbrot set, progressing down the scale of the circular “bulbs” along the real axis. This is a more extensive version of the “Mandelbrot zoom” gif in the Wiki article which uses a loop of two circles without “hair”.

First note that the Mandelbrot set itself is the black area, determined by points c, where the iteration of the defining formula always remains bounded. The “hair” is exterior to the set and is colored according to how rapidly the formula diverges under iteration.

These circles are in the set, and are called “period bulbs” in the article, because of the defining nature of the points within them. That is, they are points c, in the imaginary plane, such that iteration of x = x^2+c ( where ‘=’ means assignment, as in a programming language ) starting with x == 0 ( ‘==’ asserts equality ) converges to a cycle of fixed values, these values being 2 in number in the “2” bulb ( the first circle ) then 4 in number, then 8, 16, 32, and 64 in number in the large circle of the sixth and last frame.

This brings us to the math, and bc. Let’s go for the gusto with the “64 bulb”. Using the “click and zoom” facility in the interactive viewer, we go to the sixth bulb, i.e. the 64 bulb, and simply copy and paste the x-axis ( i.e. real part ) value into bc, and initialize x to 0:

c= -1.400968738408754
x=0

Then we iterate for a goodly number of times to assure ourselves of convergence to a stable cycle, in the belief this must happen:
( Even though bc runs interpretively, the power of a modern PC is such that this number of iterations causes a barely perceptible hitch in the response )

n=100000
for( i=0 ; i<n ; i++ ) x=x^2+c;x
.010561399880314

Now we check for a 64 cycle of values:

n=64
for( i=0 ; i<n ; i++ ) x=x^2+c;x
.010561399880314

OK! But maybe this is a repetition of a shorter cycle, so check 32:

n=32
for( i=0 ; i<n ; i++ ) x=x^2+c;x
-.000137388541270
for( i=0 ; i<n ; i++ ) x=x^2+c;x
.010561399880314

OK again!  We can now be satisfied that 64 is the true cycle value. Note that we didn’t use a lot of precision, but the “attractive cycle” is strong medicine, and we don’t need it. We are just checking the fundamentals though, and of course there are more delicate arrangements to be found.

In particular, what about the “vanishing point” of this self-similarity? It is cited in the article to crude precision as -1.401155, which can be discerned numerically, but what are its defining properties? This point remains obscure to me.

Misiurewicz points

These are defined as values of c such that k iterations of x=x^2+c give a value that repeats after n ( more ) iterations, and are designated as M_k,n, and these form vanishing points for self-similar transformations although they do not account for the seemingly fundamental one just described. Noteworthy is M_4,1  described in the Wiki article.

Here is a zoom which goes by steps of 100X magnification ( after an initial step of 10X )
The Wikipedia article on Misiurewicz points mentions … “(Even the `principal Misiurewicz point in the 1/3-limb’, at the end of the parameter rays at angles 9/56, 11/56, and 15/56, turns out to be asymptotically a spiral, with infinitely many turns, even though this is hard to see without maginification.)” ( sic ! just noticed that. ) … This is our guy, and you can see the “slow roll”, which advances by about 50 degrees in 6 steps of 100X magnification. ( I’m still working on the meaning of those angle values. )

In this case we can do a little math and come up with a way to define the M_4,1 point, at the center of the zoom, to arbitrary precision. Approaching it graphically we see the center at approximately ( -.10109636 , .95628651 ) in the complex plane.

In bc we define functions:

define f(a,b){ return( a^2-b^2 + c); }
define g(a,b){ return( 2*a*b +d ) ; }

… which are the real and imaginary parts of the formula, x^2 + (c,d) , applied to a complex value x with real and imaginary parts (a,b) . So we can proceed to apply the formula iteratively and see if we come up with a constant value after 4 iterations, as per the M_4,1 designation:

c= -.10109636
d= .95628651
x=y=0
z=f(x,y);y=g(x,y);x=z;x;y # iteration 1
-.10109636
.95628651
z=f(x,y);y=g(x,y);x=z;x;y # iteration 2
-1.0053597752027305
.7629323394437928
z=f(x,y);y=g(x,y);x=z;x;y # iteration 3
.32758616302650612570470420629841
-.57775646055620961839245967248080
z=f(x,y);y=g(x,y);x=z;x;y # iteration 4
-.32758619350801035155822390304043175425331545129536
.57775646584523271983382407623684575759993010598581
z=f(x,y);y=g(x,y);x=z;x;y # iteration 5
-.32758617964890595894029463234712218921204878613363
.57775642715823884156305664636678518208809205705010

Note that the 4th iteration approximately achieves the repeated value, but the 3rd iteration is the negative of it. So to home in on the exact value we want to adjust c so that f(f(f(f(0)))) = – f(f(f(0))). Without spelling it all out, we can do this by numerically evaluating the sum of the 3rd and 4th iterate ( which we want to be 0 ) to see how it varies with small variation in the real and imaginary parts of c . This is essentialy “Newton’s method” of finding roots. Inverting a simple 2X2 matrix tells how to vary ( c, d ) to bring this sum to 0. By iterating this estimation we can find  the correct complex value of M_4,1 to arbitrary precision.

Here’s as far as I’ve taken it so far:
( c, d ) = (
#real part
-.1010963638456221610257854457386225654638054428262534
838769311776607808407404705842748212198105167791
,
# imaginary part
.9562865108091415007710960577299774358098333365105291
700343143215005246590657167325269784107873398073
)

It’s very easy to do and could be taken to many thousands of decimal places in less than an hour, I’m sure.

I’ve got a lot more, but I want to put something out now and I do plan to continue my discussion … but let me just outline my thoughts.

The mathematical structure of the Mandelbrot set has been a matter of ongoing investigation, and is a difficult subject. One fundamental point is the “connectedness” of the set, and it has been proven that it is “connected” according to the literature. Well, I’m sure it has, but I still have questions! In particular it seems to me that these Misiurewicz points must be isolated elements of the set. Perhaps in some sense they are, since topology has more definitions than you can shake a stick at.

Anyway, I hope to be back with more pictures.

I came across the Spot it! card game a few months ago, and it didn’t take long to start wondering about the mathematics of the deck design. Here is the game with three cards displayed. Every pair of cards has exactly one matching pair of symbols, as illustrated here where the three pairings share a chess knight, a cat, and a dog.

There are 8 cards that have knights on them, and a little consideration shows that the 8×7 other symbols on these cards must be unique ( since each pair of cards has one match. )  Then there must be 57 symbols, on this fact alone. If there are 57 cards, then each of the 57 symbols can be accounted for if they each appear on 8 cards.

I got this far, then found the blog, BOWMAN IN ARABIA with the article, Math Circle Problem: Analysis of the Game “Spot it!”,  which outlines an algorithm for finding decks of PX(P+1) + 1 cards and the same number of unique symbols, with P+1 symbols on each card, for P prime.

I added a note about a solution for P=4, and I surmised that P = 2^N works along with P prime. I wrote ( and refined,  with considerable effort, ) a “brute force” search program, and verified that P=6 does not yield a solution, and proceeded to P=9, expecting the same. However, this search yielded numerous solutions. ( I let it run for several days, thinking that it would stop at 7! solutions, based on simple extrapolation. However, it was still going strong at that point and I terminated the run. ) I then surmised that P^N + 1, P prime, yields solutions, and this seems to be corroborated from what I read, and is evidently related to the “Sylow subgroups” of the Symmetric groups (aka permutation groups. )

You could say that’s the end of it, but there are a lot of “pfathinatin” details to be observed in the structure and properties of these solutions. Let us first return to the commercially available SPOT IT! deck, and then consider some other simple cases.

In fact, there are 55 cards in this deck, and it is observed that it must be obtained simply by removing two cards from the mathematically ideal solution. This is verified by the following image of a canonical arrangement of the cards, with the two “missing” cards ( they are not there when you buy them! ) … supplied by the logic explained:

On the left is the arbitrarily chosen ABCDEFGH card, whose 8 symbols are given canonical status. Note that in each of the 8 rows of 7 cards, each card contains the same symbol from the “key card” , with A=knight, B=balloon, etc. ( The “key symbol” is given upright orientation in each case. )

The top row defines 8 canonical sets of 7 symbols, ( excluding the knight, )  one of which must appear in each of the cards of every row. The second row, or “B=balloon” row, arranged in arbitrary order, defines a canonical index into each of these sets, based on the row position of its member symbols. This index is important in algorithms for constructing “solutions”,  i.e. valid SPOT IT! decks.

Then … each subsequent row is arranged so that the symbols matching the left-top-most card, the second key card, are in the same order as the “B=balloon” row, thus forming a 7X7 array of cards, excluding only the “A=knight” cards, indexed in a canonical way by the seven non-knight symbols on the two key cards. Wonderful!

Well, note that we come up with two “holes” in a very natural way, and can fill them in according to the symbol missing in their row from each of the “A row” cards, and this has been done, at great cost of manual labor.

General Principles

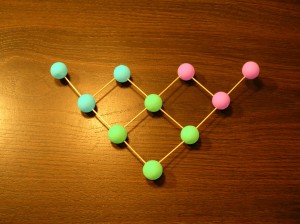
But let us return to a simpler case to illustrate some general considerations. The very simplest nontrivial case is 3 ( 2X1 + 1 ) cards with 2 symbols on each card, AB, AC, BC. However, this is a bit too simple, and the next case of 7 ( 3X2+1) cards with 3 symbols on each card is interesting but not too complicated.

It suffices to illustrate the geometric model, where each card is a vertex of a 6-d simplex ( noting that a 3-d simplex has 4 vertices, e.g. ) and each symbol corresponds to a 2-d simplex, or triangle, connecting all of the vertices representing cards with the same matching symbol.

Thus, the whole problem of constructing a deck of N X (N+1)+1 cards is seen to be equivalent to an EDGE COLORING problem on an N X (N+1)-simplex. We require the edges to be colored ( in this case) with 7 colors, such that the edges of 7 2-simplexes ( triangles) have the same (unique) color, and each vertex is shared by 3 of these.

Not sure where that gets us, but it does seem to be a helpful visualization.

Duality

In consideration of the idealized SPOT IT! deck, it appears that just as every pair of cards shares a unique symbol, so every pair of symbols shares, or appears on, a unique card. Thus every deck can be specified in a dual fashion, with a solution that corresponds to itself or another deck.

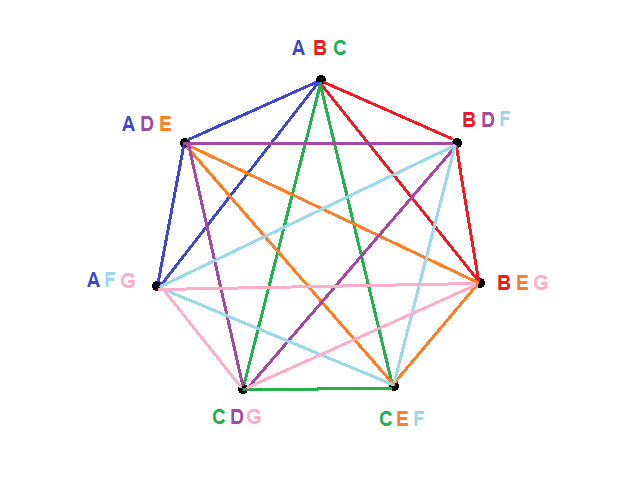
For the case of N=3 we can see a SELF-DUAL solution if we label each card with a,b,c,d,e,f,g as follows

a=ABC b=ADE c=AFG d=BDF e=BEG f=CDG g=CEF

… indicating which symbols occur on each card. Then the symbols can be specified by the set of cards on which they occur:

A=abc B=ade C=afg D=bdf E=beg F=cdg G=cef

… and we see that we have the same specification with interchange of upper and lower case. I promise you that I typed these out according to the definition, and not by rote! For higher values of N, the solutions are not all self-dual, and I haven’t explored the necessary arrangements.

Permutation of symbols

It seems clear that any solution derived by permuting the symbol values of an existing solution is valid, and will not necessarily involve the same cards, as defined by the symbols appearing on them. In the case of 7 symbols appearing 3 times each on 7 cards, we can easily permute them and “orthonormalize” them to arrive at the 7! = 5040 different results:

$ for i in `perm ABCDEFG`; do tr ABCDEFG $i <ABC | orsort; done | sort | uniq -c

168 ABC ADE AFG BDF BEG CDG CEF
168 ABC ADE AFG BDG BEF CDF CEG
168 ABC ADF AEG BDE BFG CDG CEF
168 ABC ADF AEG BDG BEF CDE CFG
168 ABC ADG AEF BDE BFG CDF CEG
168 ABC ADG AEF BDF BEG CDE CFG
168 ABD ACE AFG BCF BEG CDG DEF
168 ABD ACE AFG BCG BEF CDF DEG
168 ABD ACF AEG BCE BFG CDG DEF
168 ABD ACF AEG BCG BEF CDE DFG
168 ABD ACG AEF BCE BFG CDF DEG
168 ABD ACG AEF BCF BEG CDE DFG
168 ABE ACD AFG BCF BDG CEG DEF
168 ABE ACD AFG BCG BDF CEF DEG
168 ABE ACF ADG BCD BFG CEG DEF
168 ABE ACF ADG BCG BDF CDE EFG
168 ABE ACG ADF BCD BFG CEF DEG
168 ABE ACG ADF BCF BDG CDE EFG
168 ABF ACD AEG BCE BDG CFG DEF
168 ABF ACD AEG BCG BDE CEF DFG
168 ABF ACE ADG BCD BEG CFG DEF
168 ABF ACE ADG BCG BDE CDF EFG
168 ABF ACG ADE BCD BEG CEF DFG
168 ABF ACG ADE BCE BDG CDF EFG
168 ABG ACD AEF BCE BDF CFG DEG
168 ABG ACD AEF BCF BDE CEG DFG
168 ABG ACE ADF BCD BEF CFG DEG
168 ABG ACE ADF BCF BDE CDG EFG
168 ABG ACF ADE BCD BEF CEG DFG
168 ABG ACF ADE BCE BDF CDG EFG

… showing that the 5040 permutations of the symbol tags, ABCDEFG, result in 168 repetitions each of 30 different 7 card decks, each a solution of the SPOT IT! specification.

ABC is a file containing the original 7 card solution

$ cat ABC
ABC ADE AFG BDF BEG CDG CEF

This takes a minute to run on CYGWIN, even with todays mind-bogglingly fast processor speeds, because of the shell level logic. ( “perm” and “orsort” are C programs I wrote. )  So this is my excuse for not offering results for higher values of N.

Generating solutions 

As I mentioned above, my first investigation of the SPOT IT! problem involved writing programs to generate solutions for small values of N, where N is the number of symbols on each card of a deck comprising N X ( N-1 ) + 1 cards. I led off this discussion with a canonical arrangement of the actual commercial SPOT IT! deck,  which  provides the framework for this effort, as noted.

The cards containing two symbols, designated A and B, can be specified in a canonical arrangement which labels all the available symbols, and the solution for a full deck entails specifying additional cards, each with N of these symbols on it, that complete the deck and satisfy the unique matching condition.

Here is the top portion of the image above with numerical indexes overlayed on the symbols, according to the scheme explained:

The symbols on the A row ( other than A=knight ) are labeled according to the position of their occurrence in the second ( B=balloon ) row, which is not labelled because every label corresponds to the position of the card, 1 thru 7. Each card of the A row is labelled with a different color, indicating its column.

The third, or C=zebra, row has each symbol labeled according to its color and value in the A row. It so happens that for this case of N=8, once the C row is specified, the solution is unique. Using the color to indicate a column, as noted, the labeling generates the array specification:

… and these are the terms in which my program generates solutions. That program found 120 unique solutions in these terms, of which this one happens to be the 14th:

1 2 3 4 5 6 7
2 3 6 1 7 5 4
3 6 5 2 4 7 1
4 1 2 7 6 3 5
5 7 4 6 2 1 3
6 5 7 3 1 4 2
7 4 1 5 3 2 6

1 3 5 7 2 4 6
2 6 7 4 3 1 5
3 5 4 1 6 2 7
4 2 6 5 1 7 3
5 4 2 3 7 6 1
6 7 1 2 5 3 4
7 1 3 6 4 5 2

1 4 7 2 6 5 3
2 1 4 3 5 7 6
3 2 1 6 7 4 5
4 7 5 1 3 6 2
5 6 3 7 1 2 4
6 3 2 5 4 1 7
7 5 6 4 2 3 1

1 5 2 6 3 7 4
2 7 3 5 6 4 1
3 4 6 7 5 1 2
4 6 1 3 2 5 7
5 2 7 1 4 3 6
6 1 5 4 7 2 3
7 3 4 2 1 6 5

1 6 4 5 7 3 2
2 5 1 7 4 6 3
3 7 2 4 1 5 6
4 3 7 6 5 2 1
5 1 6 2 3 4 7
6 4 3 1 2 7 5
7 2 5 3 6 1 4

1 7 6 3 4 2 5
2 4 5 6 1 3 7
3 1 7 5 2 6 4
4 5 3 2 7 1 6
5 3 1 4 6 7 2
6 2 4 7 3 5 1
7 6 2 1 5 4 3

The C row matches, and I spot checked the D, E, etc. rows, which according to my logic must necessarily match.

And now a true confession. Note that the C row array specification is symmetric about the major diagonal. I.e. we have  1, 22, 333, 4664, 51515, etc. reading from the left column up to the right, proceeding from top to bottom. I noticed that the solutions, starting from this canonical form and using brute force search, had this form for small N, up to N=5. I found that for N=8, e.g., the brute force search bogged down hopelessly, searching through fruitless combinations, so I restricted the search to these symmetrical C row arrays, and was able to proceed up to N=9. It rankles me, but I haven’t been able to prove that this condition is necessary, however evident it seems that it must be true.

Concomitant to the symmetric C row array, we see that the other row arrays are each formed by a permutation of the columns of index values into the canonically order sets of symbols defined by the A and B rows. This is a purely empirical observation, but it certainly seems to be true in general, and so I stand in perplexity.

More on enumeration of solutions

I commented above under the “Permutation of symbols” heading,  that brute force enumeration, which I carried out for the case of 3 symbols per card, is not practical for larger values. Note that with 4 symbols per card we have 13 instead of 7 unique symbols, and 13!  =  6227020800, as compared to 7! = 5040.  However, some straightforward reasoning allows us to proceed.

Starting with the case of N=3 symbols per card, we can observe that we must have a unique ABx card, and there are then 5 choices for the third symbol, x, on that card, and each of these cases is equivalent, since the labelling of the symbols is arbitrary. Also every deck containing a different ABx card is different, so there are 5 equinumerous sets of unique decks, all different.

So it suffices to enumerate the decks containing an ABC card. We note there must be an AD card, which must be ADE, ADF, or ADG, and following the same reasoning as above, these define 3 equinumerous sets of unique decks, so now we have 15 sets of decks, each equinumerous with the deck containing ABC, ADE, and we can anticipate from the earlier enumeration of 30 unique 3 symbol decks that each of these sets has 2 unique decks.

So continuing, with ABC, ADE, we must have AFG, and we must have a BDx card, which can be BDE or BDG, so the two possible decks are :

ABC ADE AFG BDF BEG CDG CEF
ABC ADE AFG BDG BEF CDF CDG

… and we have 5*3*2 = 30 unique decks with 3 symbols on each card, given 7 unique symbols, so we move along to the case of N=4.

With 13 symbols, we see that there will be C(11,2) = 55 possible cards, ABxy, with the 11 remaining symbols taken in combination 2 at a time. Then in each case, using ABCD as our exemplar, we will have C(8,2) = 28 possible cards, AExy, and then C(5,2) = 10 AHxy cards, leaving the AKLM card, making 15400 unique sets of 4 Axyz cards. For each these sets, we can form the same number of Bxyz cards ( x,y,z != A ) so we take the case of  { ABCD, AEFG, AHIJ, AKLM } and note that each Bxyz must have one symbol from each of the last 3 in this “A set” . There must be a BEyz, BFyz, and BGyz card, and there are 3!*3! ways to assign {H,I,J} and {K,L,M} to y and z. So there are 36 “B sets”.

Now we come to the point of the matrix solution which completes a deck given canonically chosen “A & B sets”, as described above for the case of N=8, the true SPOT IT! deck. One last factor to account for is the interchange of the remaining symbols after A and B. The matrix solution assumes a canonical order for these, so that it won’t redundantly find solutions obtained by shuffling the matrices around. For N=4 this just means a factor of 2 to allow for the swapping of C and D.

Then, in the case of N=4, we get the unique matrix solution:

1 2 3
2 3 1
3 1 2

1 3 2
2 1 3
3 2 1

Which just means that given

ABCD AEFG AHIJ AKLM BEHK BFIL BGJM CE.. CF.. CG.. DE.. DF.. DG..
there is a unique solution, “up to” interchange of C and D. Note that CE, CF, CG, DE, DF, DG must each be present, and this is accounted for in the matrix solution by setting the first column always to 1,2,3 as indexes to  E,F,G in the second position of the “B cards” .

This brings us to N=8. The reasoning just adduced gives a general formula for any N, which applied to N=8 becomes, for the number of “A sets” :

C(56,7) * C(49,7) * C(42,7) * C(35,7) * C(28,7) * C(14,7) / 8!  =

56! / ( 7! )^8 / 8! = 42354925592620124113657511548409579520000

… and for the number of “B sets” for each “A set” : (6!)^6 = 139314069504000000

… throwing in the factor of 6! for the permutation of C,D,E,F,G,H and recalling that there are 120 matrix solutions to every “A & B set” specification, we have a grand total of:

509815040933983250324665926101388800612911244378112000000000000

unique 57 card SPOT IT! decks, using the same 57 symbols. And the 57! permutations of the symbols of any one of these will produce 79493377501440 copies of each of them.

In his essay, The Sand Reckoner, Archimedes specified a system of nomenclature for large numbers.  ( The greek title is yammites which is simply, “sand”. Interestingly, Liddel and Scott’s Intermediate Greek Lexicon includes yammakosioi, a “sand-hundred”, stated to be a “comic word”, presumably like “gazillion’, indicating a “countless multitude”. )

The Greeks had names for ten, hundred, thousand, and ten thousand, which was the myriad, and by composition had expressions for numbers up to the myriad myriad, which Archimedes used as the base of his system, and which we designate here by M. He called the numbers from 1 to M the first order of numbers, and using M as a unit of the second order, counted from M to M², which became the unit of the third order. Continuing in this way, he postulated M such orders, counting up to M^M.

He then called this the 1st period of orders, and continued with the 1st order of the second period counting in units of M^M up to M^M+1. Then M orders of the 2nd period count up to M^2M, and finally the Mth period counts to M^M2, which was the limit of his system.

Note that the orders of each period all count from 1 to M, so that the M periods of M orders comprise M² orders all together, accounting for M² factors of M.

This system of Archimedes is considered as something of an oddball, but it is actually familar to us in the form of our number naming system, if we take M to stand for “million” instead of “myriad myriad”.

Note that “million” derives from the Italian, “millione” meaning “grand thousand”,  i.e. a thousand thousand, so our million corresponds directly to the myriad myriad, or “grand myriad”, even though different in value. Then we see that the “long scale” or European system, which uses a million as a multiplier, starts off just like Archimedes’ system, with the numbers of the second order counting by millions up to one billion, the unit of the third order numbers, which count up to one trillion, and so on.

Well then, how well does our nomenclature keep up with Archimedes in this analogy?  The first sign of trouble ahead comes at  the end of the 1000th order, when we hit one milliatillion, as this is where the nomenclature plays its last card. Still, we make out OK up to the end of the first period, where the one millionth order ends at one milliamilliatillion.

Now in the Archimedian system, we “start fresh” at each period, so we can specify an order of each period between one and one million and get any power of a million up to a million million. In the modern “long scale” we are stuck with concatenating an extra “milliamillia” for each period, and the unit of the first order of the 5th period is

one milliamilliamilliamilliamilliamilliamilliamilliamilliamilliatillion

( I’ve been using the site: The English name of a number, for these values. Set “power of ten” and “European ruleset” . )

So I think Archimedes wins the point. But could we extend the modern nomenclature to accommodate the Archimedean scheme? This would mean extending it to one million periods, and in fact this can very easily be done.

Just as the suffix “-tillion” indicates powers of one million, we can introduce the suffix “-zillion” to indicate powers of milliamilliatillion, or one million to the one millionth power. Each period introduces a factor of one zillion, so we can call the largest number of the second period one bazillion, in analogy to one billion as a million million ( in the “long scale” ) . Then we march through trazillion, quatrazillion, etc. in one to one correspondence with the orders of the first period, and the largest number of the millionth period, which is the limit of this scheme, is one miliamilliazillion. So there you are.

RUDY RUCKER’S “SUGGESTION”

Rudy Rucker makes some cursory but pithy comments in his 1983 book, INFINITY AND THE MIND. Here is an excerpt from my copy of the Bantam paperback edition.

Regarding the highlighted recursion rules, there are two mistakes. The first is a trivial error in ii) A(1, j+1 ) = M*A(k,j) which evidently s/b ii) A(1,j+1) = M*A(1,j), noting that rule iv covers values of k > 1, ( although it allows k+1 = M+1, which we shall overlook.)

The second error is not so easily dismissed. This is in iii) A(k+1,1) = A(k,m), which s/b iii) A(k+1,1) = M*A(k,M), since A(k,j) is the GREATEST value of the jth order of the kth period, and A(k,M) is the UNIT of A(k+1,1) . I checked this out with actual recursive definitions in “bc” on cygwin, for low base values such as 3,4, and 5, so don’t doubt me!

But what about this? I think it’s all explained by the author’s  suggested improvement using rule iv*) . The modified rule, with the other rules as stated ( except for the above cited trivial correction ) does produce values of A(M,M) = M^M^M, as claimed, so it would appear that the original formulas were reverse engineered from the “improved” version.

The machinations of the latter can be easily discerned. The “highest values of the orders of the periods” ( inconsistently so called )  progess as follows:

M        M²       … M^M
M^M      M^2M      … M^M2
M^M2     M^2M2     … M^M3
…
M^M(M-1) M^2M(M-1) … M^MM

… but this seems to bear very little relation to Archimedes’ scheme, which is based on simple enumeration. The multiplier value of M comes from counting 1 thru M in each order of each period, and this is the defining principle. It is the unit of the enumeration that changes, and the numbers of all the orders are the same, namely 1 thru M.

But nevertheless ! … there is a connection, and Rucker’s modified formula is contained in the Archimedean scheme. Note the very suggestive sequence of      A(k,M) = M^Mk , where k=1 corresponds to the end of the Mth order, and k=2 corresponds to the end of the Mth period. The suggestion is namely that we consider orders and periods to be the 1st and 2nd levels of a generalized sequence of nth level periods.

Furthermore, each row comprises successive powers of the first element, as specified by rule iv*). So Rucker’s scheme gives a summary of the values reached by the jth element of the kth-level period, j and k passing from 1 to M.

Note that it would require a recursive function with M arguments to specify M levels of periods in a direct continuation of the original scheme.

It seems that Rucker must have used this reasoning, or some form of it, to derive his function, but his remarks that Archimedes “could” and “should” have made a similar specification remain puzzling.

Charles Sanders Peirce, in his essay, LOGIC AS SEMIOTIC: THE THEORY OF SIGNS, presents a diagram displaying the ten types of signs in a triangular array, like bowling pins. These are categorized by three different threefold classifications, his “three trichotomies”, which allow for the specification of 27 types, but only ten are valid. There’s a very simple rule that performs this reduction, but it is not specifically enunciated, that I can notice, even though you can see him applying it.

The Wikipedia article Semiotic elements and classes of signs makes the rule fairly clear with a diagram, but again does not specifically enunciate it, saying simply, ” many co-classifications aren’t found”.

Some years ago, in my own ruminations of the essay I cited, I realized the rule was simply this, that in each label, reduced to a three digit ternary number, abc, where a, b, and c are elements of {0,1,2}, we must have a >= b >= c. Thus when b=0, specifying an Icon, we can only have 000, 100, and 200. The logic of this is that each succesive category can only partake of a quality present in the previous category, so that the Qualisign, 000, is unique, and conversely the Argument, 222, is as well.

Realizing all this, I made a model representing the subset of the 3X3X3 cube:

This crude model is a number of years old, and its survival is no doubt partly due to its simple construction, as it is composed of exactly two identically folded paper pieces, a reflection of the symmetry of this subset of the cube. It is essentially, except for edge conditions, 1/6 of the cube, as partitioned by 3 bisecting cuts along a major diagonal. I felt that all this symmetry impinged, or ought to impinge on the significance of the categories, but I never pursued such thinking. Nevertheless, the construction does serve as a powerful mnemonic, and stands as a rival to Peirce’s own diagram.

Well, just lately, I had the thought to make a direct comparison of the two, and found that there is a direct relationship, and in fact Peirce’s tableaux does embody most of the symmetry of the cubic model, even if it doesn’t directly display the restrictive rule.

So with that preamble, here is Peirce’s tableaux marked to display the groupings of the Icons, Indexes, and Symbols:

Then here is a new model of the cubic representation using a lattice so you can see all the elements, and of course the same color coding. You can see that the Icons, Indexes and Symbols belong to three separate planes perpendicular to their defining axis:
This is suggestive, but how can we relate this lattice directly to the Tableaux? A start is to try a projection, or view along an axis of symmetry, to spread things out a little. Here is such a view of the same model:
This goes pretty far. Note that the ( green ) Indexical categories do in fact correspond to the Tableaux. ( You may believe me that the correspondence is exact. ) However, the other elements are out of whack. The three rows of this projection are not the same as the rows of the Tableaux.

We can almost rectify everything by flattening the lattice.  This only requires “unbending”  the two right angle connections between the blue and green, and the pink and green:
This is almost it! We have retained the connective character of the lattice model, and come very close to Peirce’s original representation. In fact, we could modify the Tableaux by a simple cut and paste of the Argument and Qualisign elements. But let us bow to precedent and esthetics, and simply swing the lattice elements, which have only one connection, into the “correct” place, and we have an exact correspondence without really sacrificing anything: